If you're looking for help with C#, .NET, Azure, Architecture, or would simply value an independent opinion then please get in touch here or over on Twitter.
Those of you who read my Christmas break update will know I’ve taken a slight detour into low level graphics and games programming, writing a C++ voxel engine from the ground up for fun and a challenge. I’ve continued to tinker with it when I can and have since added support for voxel based sprites. In the screenshot below the aliens, player and bullet are all made up of voxels and move around the world space in a fashion vaguely reminiscent of the classic Space Invaders game:
Though I realise it just looks like a flat textured mesh, and that a flat textured mesh would be many times more efficient than voxels for this, the ground is also made up voxels.
Of course as soon as you add sprites or anything that moves to a world you start to think about detecting collisions and doing this efficiently remains an interesting area of development with different approaches being more or less optimal for different conditions. It’s essentially a spatial organisation problem. As such although you might think “huh, collision detection, what use is that to me?” it’s not hard to see how similar indexing approaches can be useful in answering similar questions not involving games. Similarly although the A* algorithm, for example, is traditionally thought of as a gaming algorithm I’ve found myself using it in some very interesting none-gaming spaces.
In the case of collisions between sprites in my voxel engine I need to consider hundreds of objects made up of, in sum, millions of voxels spread across an indeterminate, but essentially very large and mostly sparse, three dimensional space. Pixel / voxel perfect detection between every one of those sprites is clearly going to be horrifically expensive and so typically collision detection is broken down into two phases:
- Broad range collisions – quickly draw up a shortlist of probable collisions.
- Narrow range collisions – use additional detail to filter the probably collisions resulting from the broad range pass into the actual pixel / voxel perfect collisions.
My first attempt at solving the broad range problem in my voxel engine is a common one and takes advantage of an efficient means of determining if two boxes (2d or 3d) intersect that relies on them being axis aligned – hence the axis aligned bounding box, or AABB. If that sounds complicated – don’t worry, it isn’t and I’ll explain it later.
There are many implementations of this available online and various blog posts and tutorials but I didn’t find anything that brought it all together and so what follows is a step by step guide to AABBs and how to sort them in a tree to quickly determine intersections. There is sample code provided in the form of the C++ implementation in my voxel engine and at the bottom of this post I explain how you can use this (just the AABB tree implementation) in your own code. However this post is more about the theory and once you understand that a simple implementation is fairly straightforward (though there are numerous optimisations, some of which are in my sample code some of which aren’t, that can complicate things).
For the purposes of keeping this guide simple I’m going to draw diagrams and talk about 2 dimensional boxes (rectangles) rather than 3 dimensional boxes however quite literally to add the 3rd dimension you just need to add in the 3rd dimension. Wherever x and y apply in the below add in z following the same pattern as for x and y. Hopefully that is clear in the sample code but if you have any questions you can always reach out on Twitter.
What are AABBs?
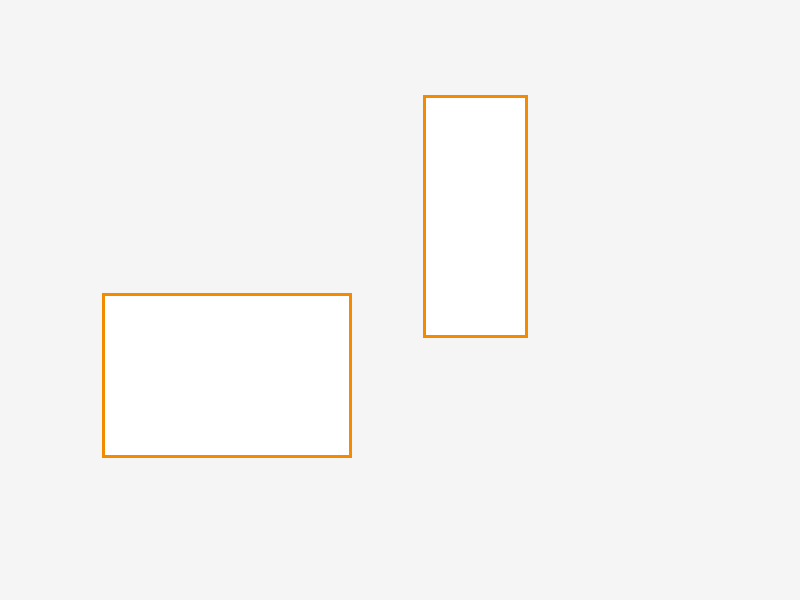
AABBs are simpler than they sound – they are essentially boxes who’s axes (so x,y for 2d and x,y,z for 3d) align / run in the same direction. The bounding part of the name is because when used for collision detection or as part of a tree they commonly contain, or bind, other boxes. The diagram below shows two simple and compatible AABBs:
In contrast the two boxes shown in the diagram below are not AABBs as their axes do not align:
A key characteristic of an AABB is that the space it occupies can be defined by 2 points irrespective of whether it is in a 2 or 3 dimensional space. In a 2 dimensional space the 2 points are (minx, miny) and (maxx, maxy).
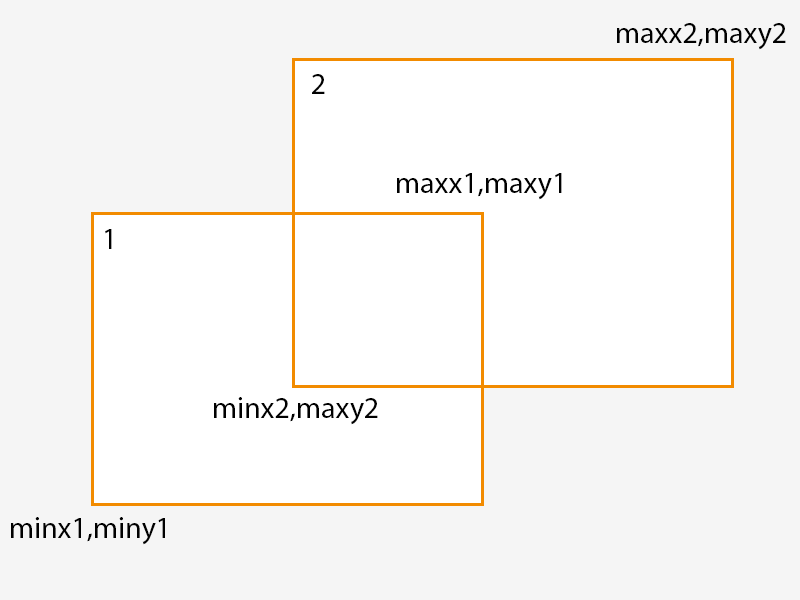
This can be used to perform a very fast check as to whether or not two AABBs intersect. Consider the two AABBs in the diagram below:
In this diagram we have two AABBs defined by a pair of points and the result of the following expression can determine whether or not they intersect:
maxx1 > minx2 && minx1 < maxx2 && maxy1 > miny1 && miny1 < maxy2
An important point to note about that expression is that it is made up of a series of ands which means that evaluation will stop as soon as one of the condition fails.
I’m fortunate working in a voxel engine in that objects in my game world are naturally axis aligned: voxels essentially being 3d pixels or tiny cubes. However what if your objects aren’t naturally aligned or are made up of shapes other than boxes? This is where the bounding part of the AABB comes in as you need to create a bounding box that encompasses the complex shape as shown in the diagram below:
Obviously testing the AABBs for an intersection will not result in pixel perfect collision detection but remember the primary goal of using AABBs is in the broad range part of the process. Having quickly and cheaply determined that the two AABBs in the diagram above do not intersect we can save ourselves the computational expense of trying to figure out if two complex shapes intersect.
The AABB Tree
Using the above approach you can see how we can quickly and easily test for collisions between two objects in your world space however what if you have 100 objects? Or 1000? No matter how efficient the individual tests comparing 1000 AABBs against themselves is going to be an expensive operation and highly wasteful.
This is where the AABB tree comes in. It allows us to organise and index our AABBs to minimise the number of AABB intersection tests that need to be made by slicing the world up using, guess what, more AABBs.
If you’ve not come across them before trees are incredibly useful hierarchical data structures and there are many variants on the basic concept (if such things interest you an excellent, if quite formal, book on the subject is Introduction to Algorithms) and before continuing it’s worth gaining a basic knowledge of the structure and terminology from this Wikipedia article.
In the case of the AABB tree presented here the root, branch and leaves have some very specific properties:
Branch – Our branches always have exactly two children (known as left and right) and are assigned an AABB that is large enough to contain all of it’s descendants.
Leaf – Our leaves are associated with a game world object and through that have an AABB. A leaf’s AABB must fit entirely within it’s parents AABB and due to how our branches are defined that means it fits in every ancestors AABB.
Root – Our root may be a branch or a leaf
The best way to illustrate how this works is through a worked example.
Constructing an AABB Tree
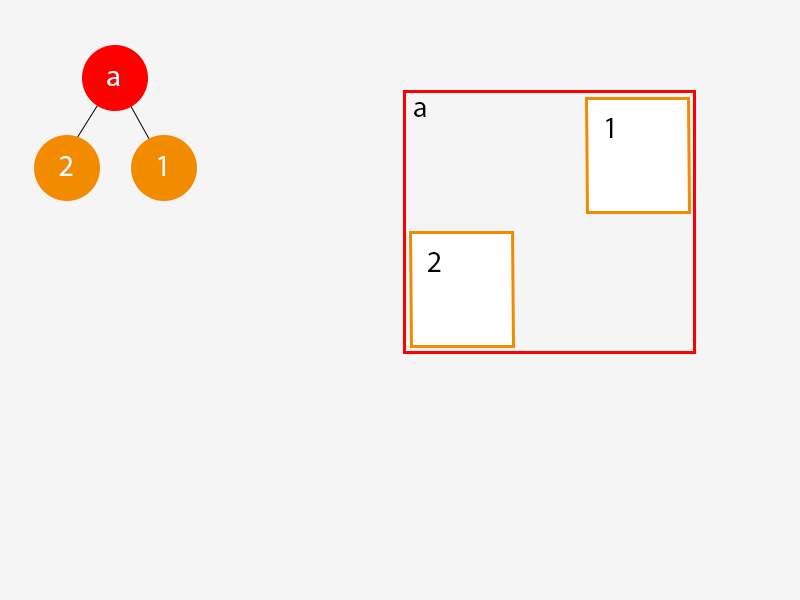
Imagine we have an empty world, and so at this point our tree is empty, to which we are adding our first object. As our tree is currently empty we create a leaf node that corresponds to our new object and shares its AABB and assign that leaf to be the root:
Now we add a second object to our world, it doesn’t intersect with our first node, and something interesting happens to our tree:
When we added the second object to our game world a number of things occurred:
- We created a branch node for our tree and assigned it an AABB that is large enough to contain both object (1) and object (2).
- We created a new leaf node for object (2) and attached it to our new branch node.
- We took our original leaf node for object (1) and attached it to our new branch node.
- We made the new branch node the root of the tree.
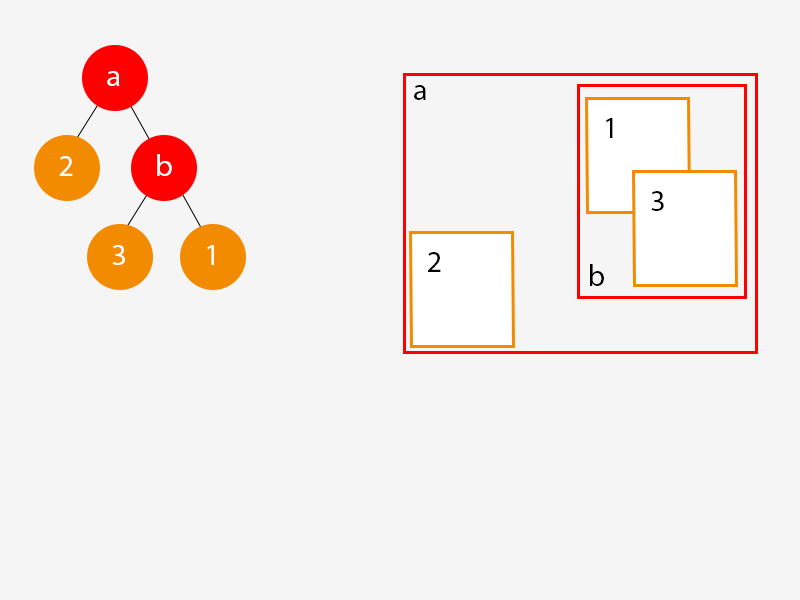
Ok. Let’s add another object to the game world and this time we’ll have it intersect with an existing object:
Again when we added this object some interesting things happened to our tree:
- We created a new branch node (b) and assigned it an AABB that encompassed objects (1) and (3).
- We created a new leaf node for object (3) and assigned it to branch (b).
- We moved leaf node (1) to be a child of branch node (b) and attached this new branch node (b) branch node (a).
- This is subtle but important: we adjusted the AABB assigned to branch node (a) so that it accounts for the new leaf node. If we hadn’t done that the AABB assigned to branch node a would no longer have been big enough to contain the AABBs of its descendants.
Essentially every time we add a new game world object we manipulate the tree so that the rules for branch and root nodes that I described earlier still apply. This being the case we can describe a generic process for adding a new game world object into the tree:
- Create a leaf node for the object and assign it an AABB based on it’s associated object.
- Find the best existing node (leaf or branch) in the tree to make the new leaf a sibling of.
- Create a new branch node for the located node and the new leaf and assign it an AABB that contains both nodes (essentially combine the AABBs of the two located node and the new leaf).
- Attach the new leaf to the new branch node.
- Remove the existing node from the tree and attach it to the new branch node.
- Attach the new branch node as a child of the existing nodes previous parent node.
- Walk back up the tree adjusting the AABB of all of our ancestors to ensure they still contain the AABBs of all of their descendants.
Step 2 in the above does beg the question: how do you find the best leaf in the tree to make the new leaf a sibling of? Essentially this involves descending the tree and evaluating the likely cost of attaching to the left or right of each branch you move through. The better the decision you can make the more balanced the tree and the cheaper the subsequent queries.
A common heuristic used here is to assign a cost to the surface area of the left and right nodes having been adjusted for the addition of the new leaf’s AABB and descend in the direction of the cheapest node until you find yourself on a leaf.
Querying the AABB Tree
This is where all of our hard work pays off – it’s very simple and very fast. If we want to find all the possible collisions for a given AABB object all we need to do, starting at the root of the tree, is:
- Check to see if the current node intersects with the test objects AABB.
- If it does and if its a leaf node then this is a collision and so add it to the list of collisions.
- If it does and it’s a branch node then descend to the left and right and recursively repeat this process.
At the end of the above your list will contain all the possible collisions for your test object and we will have minimised the number of AABB intersection checks we had to perform as we will not have descended down any pathways (and therefore all the subsequent children) that could not intersect with the test AABB tree.
In implementation it’s best not to actually use a recursive approach as this can get expensive (and could fail) on large trees. Instead just maintain a stack / list of nodes that are to be further explored as follows:
- Push the root node onto a stack (in C++ I use std::stack)
- While the stack is not empty:
- Pop from the stack
- Check and see if the node intersects with the test AABB object
- If it does then either:
- If it is a leaf node then this is a match for a collision. Add the leaf node (or its referenced object) to the list of collisions.
- If it is a branch node then push the children (the left and right nodes) on to the stack.
Understanding how to iterate over trees none-recursively can be very useful.
Updating the AABB Tree
In most (but not all) scenarios involving collision detection at least some of the objects in the world are moving. As the objects move that does require the tree to be updated and this is accomplished by removing the leaf that corresponds to the world object and reinserting it.
This can be an expensive operation and you can minimise the number of times you will need to do this if you express the movement of your world objects using a velocity vector and use this to “fatten” the AABB trees that you insert into the tree. For example take the object in the diagram below, it has a (x,y) velocity of (1,0) and has had it’s bounding AABB fattened accordingly:
How much you fatten the AABB trees is a trade off between update cost, predictability and broad range accuracy and you may need to experiment to get the best performance.
Finally as trees are updated it is possible for them to become unbalanced with some queries inappropriately requiring the traversal of many more nodes than others. One technique for resolving this is to rebalance the tree using rotations based on the height (depth from the bottom) of each node. Another is to balance the tree based around how evenly child nodes divide the parent nodes AABB. That’s slightly beyond the scope of a beginners guide and I’ve not yet implemented it myself in the sample code – however I may return to it at some point.
Sample Code
Finally their is sample code that goes along with this blog post and you can find it in my game engine. It’s pretty decoupled from the engine itself and you should be able to use it in your own code without too many problems. The key files are:
AABB.h – defines a structure for representing and manipulating an AABB
AABBTree.h – header file that defines the entry points to the tree class AABBTree and the AABBNode structure
AABBTree.cpp – implementation
IAABB.h – defines an interface that objects added to the tree must implement
To use the tree you will need to add those four files to your project and construct an instance of the AABBTree class – it’s constructor is very simple and takes an initial size (the number of tree nodes to reserve up front). Any object you want to add to the tree needs to implement the IAABB interface that simply needs to return the AABB structure when asked for. You can add, update and remove those objects with the insertObject, updateObject and removeObject methods respectively and you can query for collisions with the queryOverlaps method.
Useful Links
While researching AABB trees I found a number of useful links and these are below.
Game Physics: Broadphase Dynamic AABB Tree
AABB.cc
Box2D
In particular I found the code in the last two links very useful to read through and was able to base my own code on that, particularly the node allocation.






Hello, this explanation is a wonderful introduction to AABB Trees. There is, however, a slight mistake on the AABB intersection figure: maxy2 is written twice.
Thanks for the kind words and letting me know. I’ll get that corrected.